近日，马里兰澳门威尼克斯人网站的研究人员在13个离子量子比特上，演示了经过Bacon-Shor量子纠错编码的可纠错量子比特上的各种容错控制。

Bacon-Shor量子纠错码是最早的Shor量子纠错码的一般化版本。这篇文章使用【9，1，3】Bacon-Shor编码，是最小的可纠错任意单比特错误的编码。它和Shor编码几乎一样，主要区别在于稳定子码的测量。感兴趣的同学可以参考这篇文章[1]。量子纠错算法过程主要包括：逻辑量子态的制备和测量，逻辑比特量子门，以及稳定子码测量。这篇文章的主要目标是演示这些过程的容错特性。为了证明这一特性，文章设计了容错与非容错逻辑量子态的制备电路，容错与非容错逻辑量子门电路，以及容错与非容错稳定子码测量电路，并比较他们各自的容错表现。

图1

文中用到的样品共有15个离子量子比特。1到9量子比特，共9个量子比特，用来编码量子信息。10到13量子比特，共4个量子比特，作为测量比特。其中0和14量子比特没有参与纠错算法。该样品的平均单量子比特门保真度为99.98%，双量子比特门保真度为98.5%-99.3%，单次读取保真度为99.5%，T2 echo相干时间超过2.75s，所有量子比特之间均可以做双量子比特门。

该文首先证明逻辑量子态的制备具有容错性。图2(a)红色部分电路为非容错逻辑量子态制备电路，蓝色部分为容错逻辑量子态制备电路。制备好逻辑量子态后直接测量所有9个编码比特。通过数据处理后，图2(b)为相应的颜色的逻辑量子态的错误率。图2中，Raw指没有经过纠错的数据，Correction指纠错后的数据，Detection指丢弃掉可能发生错误的数据。纠错和丢弃数据原则，可以查看原文[0]。可以从图2中看出，纠错数据处理后，容错的态制备电路表现更好，证明其具有一定容错性；丢弃数据处理后，容错的态制备电路更进一步变好，表明纠错过程仍然有一定误差。值得注意的是，单物理比特的0态和1态的制备和测量的错误率为0.46(2)，而逻辑0态和逻辑1态的制备和测量的错误率为0.33(5)%，说明纠错变得更好。

图2

随后该文章利用非容错逻辑量子态制备电路制备魔术态（magic state）。经过纠错数据处理后，保真度达97(1)%，已经超过可以纯化的阈值92.4%。

图3

该文章也演示逻辑量子比特作为量子存储器的性质。图3为逻辑量子比特的T2*的实验数据。我们可以得到，不纠错、纠错、丢弃数据的T2*为别为26(2)ms、78(9)ms、370(160)ms，而组成这个逻辑态的单物理比特T2* 为0.6(1)s ，说明纠错效果不如不纠错。

图4

该文接着证明逻辑量子门的容错性。同样设计蓝色为容错量子门电路，红色为非容错量子门电路。经过纠错后容错量子门的保真度提高很多。

图5

该文章接着证明稳定子码的容错性。图5红色部分为非容错X稳定子码测量电路，蓝色为容错X稳定子码测量电路。右图为制备逻辑0态后经过X稳定子码电路后的逻辑Z的期望值，横坐标为测量量子比特12上人为引入Z(θ)的错误。从图中可以看出，只有容错X稳定子码测量电路在经过纠错处理后，对人为引入的Z(θ)的错误不敏感，即证明其具有一定的容错性。非容错X稳定子码测量电路和容错X稳定子码测量电路对应的错误率分别为0.85(23)%和0.25(14)%。而制备逻辑0态的错误率本身有0.23(13)%，所以容错X稳定子码测量电路几乎不引入错误。

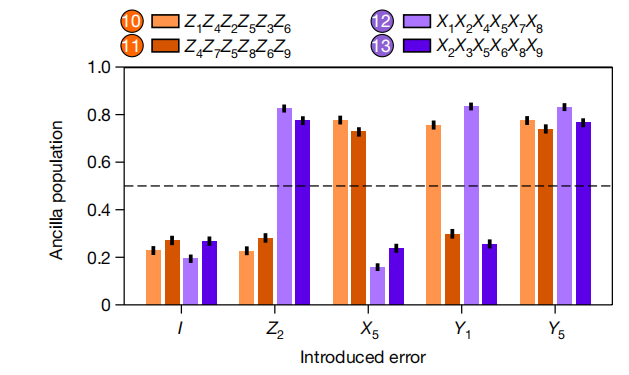
最后该文章演示引入不同的编码比特错误，观察4个稳定子码测量电路后的4个测量比特的占居数，如图6所示。例如，如果引入Z2错误，即编码量子比特2上发生Z错误，会使得测量量子比特12和测量量子比特13的占居数翻转，和实验结果一致。

总结：该文章在13个离子阱平台上演示Bacon-Shor纠错码构成一个逻辑量子比特的所有控制操作均有容错性。未来有两个里程碑的实验需要进一步研究。第一个是在两个逻辑量子比特上演示逻辑CNOT门，并证明其容错性。第二个是进行多轮稳定子码测量，演示一个不停纠错的逻辑量子比特（此文章只是演示稳定子码测量电路的容错性，并没有演示对逻辑量子比特的连续纠错）。

论文链接：

https://www.nature.com/articles/s41586-021-03928-y

（李薛刚 编译）